L’UNDERSAMPLING DEI SEGNALI SODAR
Angelo Ricotta
Il nostro mondo naturale si
comporta, per lo più, in modo analogico, almeno a livello macroscopico, per cui per interfacciarlo con computer digitali
occorre campionare i segnali analogici provenienti da esso. L’universalmente
noto teorema del campionamento dei segnali, generalmente accreditato a Nyquist e
Shannon, ma la storia è più articolata [1] [9], afferma che per ricostruire
correttamente l’informazione contenuta in un segnale a banda limitata, la
frequenza di campionamento 
deve essere almeno il doppio della più
alta frequenza 
del segnale: 
. In pratica si usa 
in quanto ci potrebbe essere ambiguità
nel ricostruire la componente associata a e anche il
ripiegamento su se stesso del bordo superiore dello spettro a causa della forma
non ideale della banda degli spettri che si riscontrano nella realtà. In questa
forma il teorema è sempre valido ma, a volte, esso viene enunciato come
dove 
è la banda del segnale. Quest’ultima
formulazione assume implicitamente che la frequenza più bassa 
del segnale sia zero, 
, altrimenti l’enunciato non è valido in generale,
come vedremo. Se la frequenza di campionamento è più bassa di 
, ovvero 
, ciascuna delle frequenze 
maggiori di 
saranno sovrapposte, ossia confuse, in
particolare, con una corrispondente frequenza 
dell’intervallo 
(pagina 1 di Fig.1) secondo la
relazione 
ossia 
con 
intero.
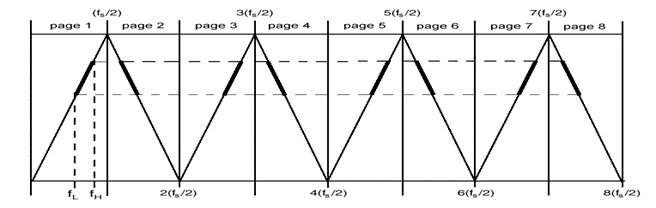
Fig.1 Ripiegamento
dello spettro attorno alla frequenza 
di Nyquist e suoi multipli [2].
Si può pensare al diagramma di
Fig.1 come ad una sequenza di pagine, ciascuna di larghezza in orizzontale,
le quali pagine possono essere ripiegate l’una sull’altra, in particolare sulla
prima, alternativamente a mo’ di “soffietto” [2]. A causa di questo fenomeno, lo
spettro di frequenze di un segnale campionato sarà replicato in tutte le
pagine. Se le frequenze dello spettro del nostro segnale da campionare sono
contenute interamente in una delle pagine esse verranno replicate in tutte le
pagine, senza però che le repliche si sovrappongano. Se lo spettro originale
già non è in prima pagina, una delle repliche spettrali del segnale campionato
sarà, in particolare, posizionata in prima pagina, secondo la relazione
surriportata, con il risultato di aver effettuato una conversione di frequenza,
evitando però il ripiegamento dello spettro su se stesso. Dalla Fig.1 si può
constatare come l’ordine delle righe spettrali viene preservato se lo spettro
del segnale originale è contenuto nelle pagine dispari, mentre viene invertito
per le pagine pari. Tutto ciò avviene in quanto il campionamento nel dominio
del tempo, che è una moltiplicazione del segnale con un pettine di impulsi
unitari, si traduce nel dominio delle frequenze nella convoluzione degli
spettri del segnale e del pettine di impulsi unitari. Un’elegante e dettagliata
descrizione, sia matematica che visuale, è data in [4]. Lo spettro completo di
un segnale campionato a banda limitata o passante è costituito da infinite
repliche dello spettro originale simmetricamente disposte intorno a multipli,
positivi e negativi, della frequenza di campionamento, come illustrato in Fig.2.
Lo spettro originale, quello della parte superiore della Fig.2, è composto da
due toni puri a 1 e 
. Si noti anche che i toni puri, originariamente posizionati in
5 e in 12, e quindi isolati nello spettro originale, sono, dopo il
campionamento, sovrapposti ai bordi dello spettro continuo. Naturalmente uno
spettro originariamente continuo, campionato per un tempo 
limitato, sarà
costituito da componenti discrete la cui risoluzione in frequenza è data da 
, che però non sono visibili in Fig.2.
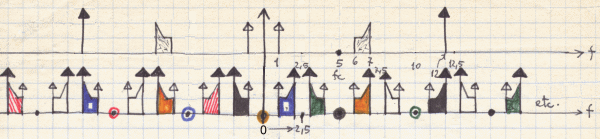
Fig.2 Repliche dello spettro di un segnale a banda limitata o passante campionato.
Il modello “a soffietto” dello spettro
di un segnale campionato si presta ad una immediata e semplice formulazione
matematica. Sia 
la banda del nostro segnale da
campionare.
Le condizioni chiave per evitare il ripiegamento dello
spettro su se stesso, per 
intero,
e 
che significa, semplicemente, che lo spettro originale del nostro segnale da campionare deve essere contenuto interamente in una delle pagine di Fig.1. In realtà lo spettro può anche essere segmentato in diverse pagine. In tal caso però occorre scrivere le condizioni di cui sopra per ogni segmento e debbono esserne verificate altre affinché i segmenti campionati non si ripieghino gli uni sugli altri.
La connessione tra i numeri di
pagina 
e 
è data dalla relazione 
Isolando dalle diseguaglianze di cui sopra
abbiamo
(1)
e quindi eliminando otteniamo
da cui
(2)
Queste sono le formule fondamentali per l’undersampling o sottocampionamento, anche se io, nella mia nota originale [3], non uso nessuno dei due termini perché, a suo tempo, non mi ero preoccupato di coniare una specifica terminologia per questa operazione.
Per esempio, sia 
e 
. Applicando la (2) abbiamo 
, ovvero 
, e quindi dalla (1) si ottengono tutte le frequenze permesse
di campionamento, ossia 
: 
, 
: 
e, naturalmente, 
: 
. Come anticipato, l’ordine delle righe dello spettro del
segnale a banda passante, ribaltato in prima pagina, sarà rovesciato o meno a
seconda della posizione dello spettro del segnale originale rispetto alla
frequenza di campionamento
scelta: se il corrispondente 
è dispari
l’ordinamento si conserva, se invece è pari l’ordine è invertito.
Notare che per
eseguire un corretto undersampling non si possono usare tutte le frequenze di
campionamento 
, infatti nell’esempio di cui sopra questa scelta
condurrebbe a 
che è ovviamente sbagliata. Se siamo
interessati solo all’estremo inferiore 
delle frequenze di campionamento, sostituendo
la (2) nella (1) il termine di sinistra fornisce
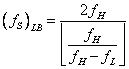(3)
che coincide con quella riportata
in [4]. Un’espressione equivalente alla (1), ma nel dominio del tempo, è data
in [5]. Non abbiamo usato il segno uguale in (1) e in (2) per evitare possibili
sovrapposizioni e ambiguità ai bordi dello spettro, ma se la potenza al di
fuori dell’intervallo aperto 
è zero o trascurabile
possiamo scrivere 
e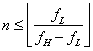 
, ovvero dobbiamo prendere in considerazione la reale forma
dello spettro a banda passante per evitare ambiguità e per minimizzare
gli errori ai suoi bordi. È possibile dare alla (3) una forma differente. Sia 
e chiamiamolo “indice di banda”.
Consideriamo la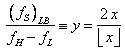 
. Il dominio di 
is 
, inoltre si ha 
e quindi 
. Il dominio di 
è 
e il suo diagramma è mostrato in Fig.3.
Notare che per 
e non a 
.
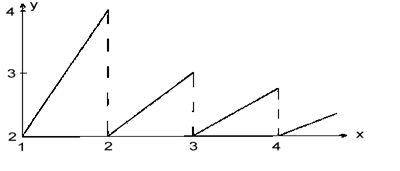
Fig.3 Estremo inferiore della frequenza di campionamento normalizzata rispetto all’indice di banda.
In un recente articolo [6] sono
state riportate due formule 
e 
per calcolare una
possibile frequenza 
per l’undersampling di un segnale a
banda passante, note la portante 
, e la banda 
. La procedura di calcolo è la seguente: in prima
approssimazione si pone 
, si inserisce questo valore in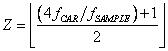 
e quindi si usa questo valore intero di
, che è approssimato per difetto, per calcolare il
vero . Penso che questo calcolo, nell’ambito di una illustrazione
dei concetti dell’undersampling o sottocampionamento, non abbia alcuna utilità
e anzi sia fuorviante almeno per due ragioni: la prima è che esso non è più
semplice della procedura richiesta dalle (1) e (2), la seconda, e peggiore, è che esso
fornisce un unico valore per la frequenza di campionamento invece di tutti gli
insiemi permessi di frequenze, inoltre la frequenza calcolata non è neanche l’estremo
inferiore, ma è solo quella particolare frequenza di campionamento per cui le
repliche spettrali del segnale campionato vengono posizionate al centro delle
pagine di Fig.1. Le formule surriportate esprimono quest’ultima proprietà in
modo poco trasparente e sono anche
farraginose come algoritmo, contrariamente alla solare logicità delle
(1) e (2). Infatti si prenda 
e 
. Essendo 
e 
, come nel precedente esempio, avremo 
, invece l’estremo inferiore delle frequenze di campionamento
è 
. Se i dati a nostra disposizione sono solo e è comunque facile passare al metodo
generale, dato dalle (1) e (2), ponendo 
e 
ed eseguendo i calcoli
nel modo già indicato. Comunque
le formule e si deducono facilmente dalla . Per
definizione è , quindi è sempre soddisfatta
in quanto implicitamente contenuta nella diseguaglianza sinistra della (1): notare
che non si può usare ogni per l’undersampling, come
già mostrato, in quanto occorre soddisfare entrambi i vincoli della (1). Per
dedurre , assumiamo 
, ossia prendiamo la media aritmetica dei due estremi
della (1). Tramite le seguenti manipolazioni algebriche otteniamo: 
.
Dato che 
, sostituendo 
dedotta dalla (1), finalmente
otteniamo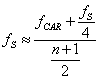 
. La sostituzione produce, come
aspettato, una più piccola della
media aritmetica assunta in partenza. Alla fine si ha 
e quindi 
con 
. Questa deduzione si può eseguire in modo più diretto
considerando che lo scopo del calcolo di questa specifica è quello di
posizionare le repliche spettrali del segnale campionato al centro delle pagine
di Fig.1. Dalle condizioni chiave [3] dobbiamo
porre 
da cui 
.
Anche nelle applicazioni pratiche è importante calcolare tutte le frequenze permesse di campionamento, in quanto possono esserci, nella specifica applicazione, dei vincoli che ci impongono l’uso di un particolare intervallo di frequenze di campionamento, per cui è sempre meglio affidarsi alla procedura generale per eseguire questo calcolo.
Il mio interesse per l’elaborazione dei segnali iniziò a metà del 1975 quando iniziai a lavorare alla mia tesi di laurea in Fisica [7] che consistette nel progetto e realizzazione di un SODAR per l’uso in studi di dinamica dello strato limite atmosferico. Per l’hardware seguii, basilarmente, il lavoro di E.J.Owens [8], aggiungendovi diverse soluzioni originali, ad ogni modo io sono stato il primo, in Italia, a progettare e costruire, personalmente, un sistema SODAR ben funzionante e ancora adesso, dopo quasi trent’anni, diverse persone continuano ad utilizzare le idee scientifiche e le soluzioni tecniche da me elaborate in quegli anni, alcune delle quali sono descritte in [3][7][10], anche se non tutti costoro lo vogliono ammettere. SODAR è l’acronimo di SOund Detecting And Ranging ed esso è un RADAR a onde acustiche che emette nell’atmosfera brevi pacchetti acustici i quali vengono diffusi dalla turbolenza. L’intervallo temporale di ripetizione dei pacchetti acustici è, normalmente, tra 3 e 6 secondi in funzione dell’intervallo spaziale da esplorare. L’emettitore è, usualmente, un altoparlante di potenza, posto al fuoco di un paraboloide per microonde il quale, a sua volta, viene racchiuso all’interno di uno schermo acustico per attenuare il rumore ambientale. Vi sono anche SODAR con antenne costituite da schiere di altoparlanti. Rispetto all’intervallo di frequenze emesse vi sono, fondamentalmente, due generi di strumenti: SODAR a bassa e ad alta frequenza. Tipicamente, l’intervallo basso di frequenze è 1000-3000 Hz, quello alto 5000-7000 Hz. In Fig.4 e Fig.5 sono mostrate le antenne di recenti versioni di SODAR che ho contribuito a progettare: le grandi antenne tronco-coniche di Fig. 4 sono quelle a bassa frequenza, mentre le tre piccole antenne horn-reflector di Fig.5 sono quelle ad alta frequenza.
Fig.4 Antenne del SODAR a bassa frequenza
Fig.5 Antenne del SODAR ad alta frequenza
Durante il 1976 e per diversi
anni, la prima versione di SODAR che progettai e costruii personalmente, e che
miglioravo continuamente, fu estensivamente utilizzata in parecchie campagne di
misura dalle quali emerse la necessità e di un efficiente campionamento del
segnale e dell’elaborazione in tempo reale dei dati. La prima esigenza nasceva
anche dal fatto che avevamo computer un po’ antiquati con A/D limitati e
modeste unità di registrazione digitali, la seconda invece proveniva dalle
necessità sorte nell’ambito del controllo dell’inquinamento atmosferico in cui
sarebbe stato utile conoscere i profili di vento in tempo reale. Il SODAR è
capace di produrre una soverchiante quantità di dati, anche per gli attuali standard,
specialmente se si vogliono registrare, oltre ai dati elaborati, anche quelli
grezzi, in previsione di analisi più approfondite. Inoltre si ha, a volte,
l’esigenza di registrare i dati continuamente per giorni e anche per mesi. Cosicché
dovevo ridurre, in qualche modo, l’entità dei dati da campionare senza però
diminuire o perdere l’informazione rilevante. La soluzione fu raggiunta per
approssimazioni successive. Il mio primo approccio fu hardware nel senso che
realizzai, nel 1980, un’audio eterodina che
traslava in basso lo spettro dell’eco. Si provò anche la decimazione dei dati
campionati, confrontando gli spettri prima e dopo e osservando empiricamente
che, in certe condizioni, il risultato era una traslazione verso il basso delle
armoniche dello spettro senza alterare la potenza delle componenti. Infine,
agli inizi del 1981, m’imbattei in [2], p.230, e immaginai che il modello “a
soffietto” aveva un’utile formulazione matematica in termini delle formule
fondamentali (1) e (2) per il
sottocampionamento surriportate. Solo molto tempo dopo lessi [4] e [5] e
realizzai che almeno la (1), anche se sotto un’altra forma, era già nota. In
questi testi l’argomento era trattato un po’ sotto tono e in modo differente (non vi appare il termine
undersampling ma “bandpass sampling theorem”) e parziale e senza una
dimostrazione esplicita, invece io penso che la mia dimostrazione sia di
un’evidenza palmare. In [4] la formula fondamentale viene enunciata in una
forma diversa e nel dominio del tempo invece che in quello delle frequenze,
come ho fatto io. Inoltre non
è data la formula per . In [5] il “bandpass sampling theorem” è elencato tra
i problemi da risolvere per i lettori e la formula mostrata si riferisce solo
alla cosiddetta “frequenza critica di campionamento” (3), ma uno dei termini
potrebbe suggerire, ad un lettore attento, il modo di calcolare . A quel tempo, per quanto ne so, le persone che
lavoravano sui SODAR non usavano la tecnica dell’undersampling per campionare l’eco,
e anzi persino
Il segnale emesso dal SODAR è un
treno d’onde sinusoidali, tipicamente della durata di 100 millisecondi e con
ripetizione di 6 secondi. I canali di ricezione si aprono dopo l’emissione del
pacchetto acustico. In generale, il segnale ricevuto è fortemente modulato in
ampiezza ma a bassa frequenza, l’ampiezza in frequenza dello spettro viene
allargata dalla turbolenza e le righe
spettrali sono anche spostate in frequenza a causa dell’effetto Doppler, inoltre
l’eco è immersa nel rumore ambientale, le cui caratteristiche di fondo
dipendono dal sito in cui è allocato il SODAR. Con il SODAR è possibile
visualizzare la turbolenza atmosferica e misurare il profilo verticale della
velocità del vento e della sua direzione fino a circa 
ai primi zeri, dove 
è la durata del pacchetto. Nel nostro
caso 
e quindi 
centrato su 
, la frequenza trasmessa. Lo spettro di potenza del segnale
ricevuto, quando il rapporto segnale rumore è molto buono, appare come in Fig.6,
per un dato segmento di dati.
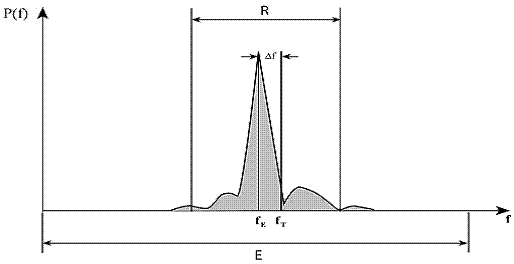
Fig.6 Spettro di potenza del segnale ricevuto con ottimo rapporto S/N
Il nostro scopo è quello di
misurare I profili verticali di velocità e direzione del vento e di intensità
della turbolenza per ogni scansione o per un certo numero di scansioni mediate,
ad un certo numero di livelli di altezza. Per calcolare in modo affidabile
queste quantità occorre campionare il segnale per renderlo disponibile
all’analisi computerizzata. Prima del campionamento però è meglio filtrare il
segnale con un filtro banda passante con larghezza di banda 
, come mostrato in Fig.6, per evitare di campionare
anche un eccessivo rumore fuori banda. Inoltre io adotto anche l’accorgimento
di agganciare la frequenza di campionamento a
quella trasmessa per compensare
un’eventuale deriva di quest’ultima che inciderebbe direttamente sulla
precisione della misura del vento. Ulteriormente, quando le bande delle
frequenze delle tre antenne sono ben separate ed esse, nell’insieme, soddisfano
i requisiti dell’undersampling, i tre segnali ricevuti vengono miscelati tutti insieme
[10] prima del campionamento riducendo, in tal modo, di un terzo la frequenza
di campionamento. In una configurazione particolare l’intera larghezza di banda
dei tre segnali del SODAR a bassa frequenza è di 
cosicché i numeri sono gli stessi del
precedente esempio eccetto che per le unità di misura, non influenti in questo
discorso. Questo è il momento in cui l’undersampling o sottocampionamento entra
in scena: il rapporto 
determina, nell’esempio mostrato, il massimo
fattore di riduzione, che possiamo ottenere, nell’entità dei dati campionati,
il che significa oltre che un grande risparmio di memoria anche una ulteriore notevole riduzione della frequenza di
campionamento (la prima si ottiene, laddove possibile, con la miscelazione dei
tre segnali), ciò che permette l’elaborazione in tempo reale dei dati con
strumentazione di più basso costo. Dopo aver sottocampionato il segnale di ogni
scansione, lo si suddivide in un certo numero di segmenti e ad ogni segmento si
applica
Nella modalità in retrodiffusione, ovvero ricevitore coassiale o coincidente con il trasmettitore, la velocità del vento è data da
(4)
dove 
è la velocità del suono, la frequenza trasmessa e 
la frequenza ricevuta. La formula (4) è
un’approssimazione al primo ordine ma più che buona per lo strato limite in cui
. Generalmente la frequenza ricevuta è definita come
il momento primo normalizzato dello spettro dell’eco
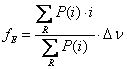
in cui 
è l’intervallo
mostrato in Fig.6, 
è
la potenza dell’
-ma componente
e 
è la risoluzione dello spettro. In una tipica
configurazione triassiale le antenne vengono posizionate come in Fig.7
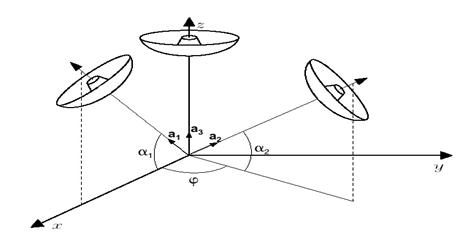
Fig.7 Orientazione delle antenne di un SODAR triassiale
Avendo calcolato le tre
componenti assiali 
, 
, della velocità del vento 
con la formula (4), occorre
trasformarle, per l’uso che se ne fa in meteorologia, in componenti cartesiane 
, , dirette rispettivamente lungo gli assi 
di un riferimento ortogonale, spesso
orientato secondo i punti cardinali. Per definizione 
e 
in cui 
e 
sono, rispettivamente,
i versori degli assi delle antenne e degli assi cartesiani. Si ha
(5)
nelle quali usiamo la convenzione della somma per gli indici ripetuti nei prodotti.
Gli 
, sono i coseni direttori tra gli assi indicati, per cui si
ha 
con 
. Dato che conosciamo le 
dalla (4), noti anche i coefficienti
geometrici 
, siamo in grado di risolvere le (5) rispetto alle tre
incognite 
. Per le particolari orientazioni mostrate in Fig.7, abbiamo
per cui
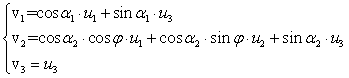
Risolvendo rispetto alle finalmente otteniamo
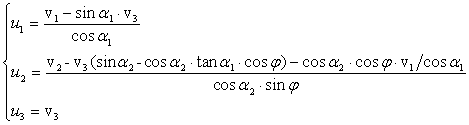
Alla fine, ciò che era iniziato
sottocampionando i segnali SODAR ha dato i suoi frutti. È infine possibile registrare,
visualizzare, stampare profili della velocità e della direzione del vento e
dell’intensità della turbolenza nello strato limite atmosferico, fino a circa
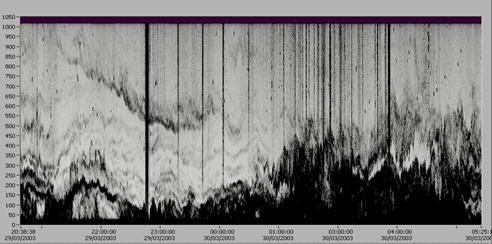
Fig.8 Profilo verticale dell’intensità del segnale verticale retrodiffuso rispetto al tempo.
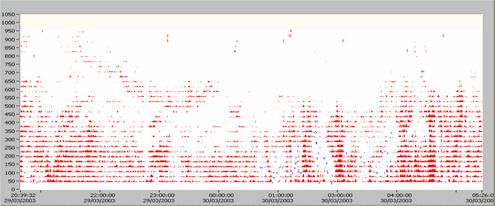
Fig.9 Profilo verticale della componente verticale del vento rispetto al tempo.
BIBLIOGRAFIA
[1] Abdul J. Jerry, “The Shannon Sampling
Theorem – Its Various Extensions and Applications: A Tutorial
Review”, Proc. of IEEE, vol.65, no. 11,
November 1977.
[2] Julius S. Bendat, Allan G. Piersol,
“Random Data: Analysis and Measurement Procedures”, Wiley-Interscience, 1971,
(p.230).
[4] E.
Oran Brigham, “The Fast Fourier Transform”, Prentice-Hall, Inc., 1974, (p.87).
[5] “Reference
Data For Radio Engineers, Fifth Edition”, Howard W. Sams & Co., Inc., ITT,
1970, (p.21-14).
[6] Bonnie
Baker, “Turning Nyquist upside down by undersampling”, EDN 12 May 2005.
[7] Angelo Ricotta, “Sviluppo di un radar acustico e sue applicazioni allo studio della dinamica dello strato limite planetario”, Tesi di Laurea in Fisica, Università di Roma, Ottobre 1976.
[8] E. J. Owens, NOAA MARK VII Acoustic Echo Sounder,
NOAA Tech. Mem.,
[9] P. L. Butzer, J. R. Higgins, R. L. Stens,
“Sampling theory of signal analysis”, Development of Mathematics 1950-2000,
Editor J. P. Pier, Birkhäuser, 2000.
[10] A. Ricotta, M. Berico, “Sodar tristatico”, LPS 80-6, LPS-CNR, Frascati, 1980.