LA FACCENDA DELL’UNDERSAMPLING

Angelo Ricotta – Roma, Italia

a.ricotta@isac.cnr.it

ENGLISH VERSION

L’articolo “Turning Nyquist upside down by undersampling” a firma di Bonnie Baker, EDN 12 Maggio 2005, mi ha fatto tornare a mente degli avvenimenti di parecchi anni fa concernenti il mio coinvolgimento nell’uso di questa particolare tecnica di campionamento di segnali banda-passante (undersampling = subsampling, sottocampionamento, subcampionamento, sub-Nyquist, super-Nyquist, campionamento armonico) e il fatto che alcune persone si comportarono poco correttamente in quelle circostanze. Anche se è passato molto tempo è bene ribadire alcune documentate verità, prima che il tempo intorbidi troppo le acque e i testimoni non siano più reperibili. Innanzitutto occorre notare che nell’articolo citato sono riportate due formule: e che permettono di calcolare una singola frequenza per l’undersampling di un segnale banda passante. Questo fatto mi ha sorpreso in quanto io ho iniziato ad usare la tecnica dell’undersampling all’inizio degli anni ottanta e, dopo qualche anno, avevo persino messo per iscritto (ciò che non mi accade di frequente) i miei risultati in una nota (Angelo Ricotta, “Considerazioni sulla digitalizzazione e l’elaborazione dei segnali SODAR”, Nota Interna, IFA-CNR, Luglio 1983) in cui fornivo due semplici e pratiche formule per calcolare tutte le frequenze permesse (e non una sola!) per l’undersampling di un dato segnale passa-banda. Mi è sembrato molto strano che dopo più di 22 anni qualcuno ignorasse risultati senz’altro più versatili delle formule riportate nell’articolo pur essendo, le mie formule, altrettanto semplici matematicamente e quindi da usare. Inoltre il mio rapporto era sicuramente noto nella comunità italiana che si occupava di SODAR e le mie formule, e persino la mia particolare dimostrazione matematica di esse, venivano inserite in scritti di certuni e anche in tesi di laurea senza mai citare, scorrettamente, la fonte. Infine le formule furono comunicate, da me personalmente, ad alcune persone negli USA. Infatti il 10 Ottobre e il 7 Dicembre del 1991, anche per far cessare gli abusi suddetti, inviai in successione due lettere, contenenti le mie formule sull’undersampling, a EDN Signals & Noise Editor, ma non ricevetti mai risposta. Il 25 Marzo del 1994 partecipai, a Roma, ad un seminario della Burr-Brown Corp. di Tucson, Arizona. In quell’occasione spiegai ai due relatori le mie formule sull’undersampling, avendo notato che l’argomento era mal trattato nel testo che ci avevano fornito al seminario. Uno dei relatori, il Sig. Jason Albanus, mi suggerì di inviare le mie formule ad un tale Sig. Jerry Horn, della sede di Tucson, Arizona, della Burr-Brown, in quanto, mi disse, era lui che si occupava di compilare i testi tecnici per i seminari e che sarebbe stato senz’altro interessato a inserirvi le mie formule. Inviai la lettera, ma il recipiente non si degnò mai di darmene ricevuta. Senonché l’11 Luglio del 1994, su Electronic Design, apparve un articolo da parte di George Hill della Burr-Brown Corp., Tucson, Arizona, nel quale, a p.77, egli esponeva le mie formule sull’undersampling, esprimendosi nel seguente modo: ”In un recente seminario applicativo tenuto dalla Burr-Brown a Roma, Italia, uno dei partecipanti ha suggerito un approccio per calcolare le appropriate frequenze di campionamento per l’undersampling di qualsiasi specificato intervallo di frequenze d’ingresso. Egli ha offerto le sue idee affinché fossero incluse in futuri seminari, ma non ci ha autorizzato ad usare il suo nome [sic!]. Ecco il suo approccio…”. Naturalmente il “famoso” partecipante al seminario ero io e a me era sembrato più che ovvio che il Sig. George Hill e chiunque altro avrebbe dovuto citare il mio nome insieme alle mie formule, lapalissiano! Scrissi quindi al Sig. George Hill, il 13 Settembre 1994, invitandolo a rettificare la sua comunicazione e a citare il mio nome ogni volta che avesse usato le mie formule, ma egli non mi rispose né, per quel che ne so, fece alcuna rettifica e non so come si sia regolato in seguito, ossia se ha continuato ad utilizzare pubblicamente le mie formule senza citarmi o meno. Copie di tutte queste lettere sono ancora in mio possesso, come si può vedere dalle riproduzioni inserite nel sito.

È ora adesso che io illustri le “famose” formule. Non sto a rifare tutto il discorso da capo. L’essenziale è contenuto nel Rif.4 che ho inserito in questo stesso sito. In definitiva le formule sono l’immediata traduzione matematica del “modello a soffietto” (Rif.2) dello spettro di un segnale campionato, fenomeno che è diretta conseguenza dei teoremi di Shannon e Nyquist: sembra che il teorema del campionamento venisse formulato da Nyquist nel 1928 e più formalmente dimostrato da Shannon nel 1949, pertanto il merito più grande, ovviamente, spetta a loro. Per quanto riguarda me, cominciai ad interessarmi all’elaborazione dei segnali a metà del 1975 quando iniziai a lavorare alla mia tesi di laurea in Fisica (Rif.5) che consisteva nella progettazione e realizzazione di un sistema SODAR per l’uso in studi sulla dinamica dello strato limite planetario. La mia guida per la progettazione dell’hardware fu fondamentalmente il lavoro fatto da E.J.Owens (Rif.6), anche se io vi aggiunsi diverse soluzioni originali. Il SODAR era pronto a febbraio del 1976 e lo si utilizzò per diversi anni in parecchie campagne di misura. Naturalmente io andavo continuamente perfezionandolo e, ad un certo punto, emerse la necessità di studiare un sistema di campionamento e di elaborazione dei dati più efficiente, anche perché disponevamo solo di vecchi computer con relativamente lenti A/D e limitate unità di registrazione digitale, la necessità aguzza l’ingegno! Il mio primo approccio a questo problema fu hardware, non feci altro che utilizzare il noto concetto dell’eterodina applicandolo a segnali nella banda audio, tramite un moltiplicatore analogico e filtrando la banda base del segnale traslato in frequenza (Rif.4). Questo modulo era associato anche ad un altro dispositivo da me ideato che generava impulsi di campionamento in rapporto razionale con una frequenza data, il che permetteva di scegliere la frequenza di campionamento più opportuna sincronizzata al segnale trasmesso dal SODAR. Queste soluzioni risolvevano in un sol colpo una molteplicità di problemi tecnici che qui non posso dettagliare. Essendo stato io il primo in Italia a realizzare un sistema SODAR perfettamente funzionante molti hanno usufruito, e continuano oggi ad usufruire, delle idee scientifiche e delle soluzioni tecniche da me escogitate e, nonostante io le abbia tutte documentate, mai mi sono state esplicitamente riconosciute da un certo numero di queste persone.

Naturalmente la soluzione del problema del sottocampionamento fu raggiunta per approssimazioni successive e i passi finali avvennero tra il 1980 e il 1981 quando m’imbattei nel Rif.2, il cui grafico, a p.230, mi fece pensare che il famoso “soffietto” (Rif.4) avesse un’utile formulazione matematica dalla quale dedussi le formule del sottocampionamento. Per correttezza devo dire che qualche anno dopo mi capitò di leggere i Rif.1 (p.21-14) e Rif.3 (p.87) e realizzai che, almeno la formula fondamentale era già nota, anche se nei libri citati era espressa in modo diverso e parziale e anche un po’ sottotono (inoltre ci si riferiva al “bandpass sampling theorem” e non vi compariva la dizione “undersampling”). Nel Rif.1 si riporta la sola formula fondamentale in una forma diversa ed espressa nel dominio del tempo anziché in quello delle frequenze, come ho fatto io, inoltre manca la determinazione del parametro . Nel Rif.3 il “bandpass sampling theorem” è citato tra i problemi da risolvere per il lettore. La formula esibita riguarda la cosiddetta frequenza critica di campionamento e non tutte le possibili, un termine della formula però potrebbe suggerire, ad un lettore attento, come si può calcolare . Ad ogni modo in entrambi i riferimenti non viene riportata alcuna dimostrazione. Io trovo la mia particolarmente semplice e ingegnosa. Pertanto, alla luce di tutti questi fatti, il mio piccolo contributo al sottocampionamento lo si può definire chiarificatore e semplificatore, particolarmente adatto all’uso pratico, ma non dovrebbe essere sottovalutato o ignorato o peggio usurpato.

E adesso entriamo un po’ nel tecnico.

Siano e rispettivamente la frequenza più bassa e quella più alta di un segnale banda-passante.

Il “modello a soffietto” dello spettro di un segnale campionato impone che si abbia e , con intero, affinché lo spettro non si ripieghi su se stesso. Semplici manipolazioni forniscono la formula fondamentale in cui . Per esempio sia , . Applicando la seconda delle formule di cui sopra si ha , ovvero , e quindi dalla prima ricaviamo tutte le possibili frequenze di campionamento: : , : e, naturalmente, : . Sempre in base al “modello a soffietto” dello spettro di un segnale campionato l’ordine delle armoniche dello spettro convertito in frequenza del segnale banda-passante può essere invertito o meno a seconda della posizione del segnale originale rispetto alla frequenza di campionamento scelta : se il corrispondente indice è dispari l’ordine è conservato se è pari l’ordine è invertito. L’importanza di questi calcoli risiede nel fatto che non sempre si vuole il segnale nella posizione minima dello spettro, ma a volte si può avere l’esigenza di doverlo posizionare in un’altra banda di frequenze e comunque è bene sapere che è facile calcolare questa possibilità. Se invece delle frequenze estreme dello spettro di frequenza abbiamo la banda e la frequenza portante , come viene assunto nell’articolo di Bonnie Baker, possiamo porre e , che ci forniscono le e con le quali possiamo eseguire i calcoli con le formule da me fornite e che ci danno tutte le frequenze permesse di campionamento. Se invece ci limitiamo al calcolo suggerito da Bonnie Baker, essendo e , otteniamo il solo valore , che oltretutto non è la minima frequenza possibile ma solo un po’ inferiore alla media aritmetica degli estremi dell’intervallo più basso di frequenze permesse, precisamente è la frequenza di campionamento che centra le repliche dello spettro nelle pagine ( vedi Fig.3, p.5, Rif.4) . Comunque le formule e possono essere facilmente dedotte da . Infatti, per definizione è e quindi, come si può vedere immediatamente, deve essere sempre soddisfatta: si noti però che non si può usare qualsiasi frequenza di campionamento che soddisfa la per eseguire correttamente il sottocampionamento in quanto occorre soddisfare non uno ma due vincoli come indica la formula fondamentale surriportata. Per dedurre anche , si assuma , quale media aritmetica degli estremi.

Si ha 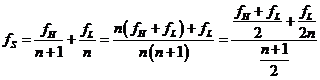. Ponendo e sostituendo otteniamo 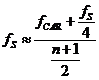. La sostituzione produce una un po’ più bassa della media aritmetica assunta prima, come avevo già anticipato. Infine si ha e quindi con . Un modo più perspicuo di ottenere è quello di sfruttare il fatto che essa permette il centraggio delle repliche dello spettro del segnale campionato nelle pagine e dei suoi multipli (Fig.3, p.5, Rif.4).

Deve essere da cui .

Questa nota in italiano è un po’ più estesa di quella in inglese perché l’ho scritta dopo e quindi vi ho aggiunto delle notizie che inizialmente non avevo ritenuto essenziale inserire nella prima. Se avrò un po’ di tempo cercherò di completare le notizie sulle mie peripezie “tecnico-scientifiche”, magari anche su altri argomenti.

Bibliografia

1. “Reference Data For Radio Engineers, Fifth Edition”, Howard W. Sams & Co., Inc., ITT, 1970, (p.21-14).

2. Julius S. Bendat, Allan G. Piersol, “Random Data: Analysis and Measurement Procedures”, Wiley-Interscience, 1971, (p.230).

3. E. Oran Brigham, “The Fast Fourier Transform”, Prentice-Hall, Inc., 1974, (p.87).

4. Angelo Ricotta, “Considerazioni sulla digitalizzazione e l’elaborazione dei segnali SODAR”, Nota Interna, IFA-CNR, Luglio 1983, (pp. 4-7).

5. Angelo Ricotta, “Sviluppo di un radar acustico e sue applicazioni allo studio della dinamica dello strato limite planetario”, Tesi di Laurea in Fisica, Univ. di Roma, 1976.

6. E. J. Owens, NOAA MARK VII Acoustic Echo Sounder, NOAA Tech. Mem., Boulder, Colo., 1975.