A STORY ABOUT UNDERSAMPLING

Angelo Ricotta – Rome, Italy

a.ricotta@isac.cnr.it

VERSIONE ITALIANA

In the article “Turning Nyquist upside down by undersampling” by Bonnie Baker, EDN 12 May 2005, are reported the two formulae and to compute an allowable sampling frequency for undersampling (bandpass sampling, subsampling, downsampling, sub-Nyquist, super-Nyquist, harmonic sampling) a bandpass signal. I was surprised by that because I have been using the undersampling technique since the beginning of the eighties and even wrote a report (Angelo Ricotta, “Some remarks on the sampling and processing of SODAR data”, Technical Report, IFA-CNR, July 1983) where I gave two simple and practical formulae to compute all the allowable sampling frequencies for undersampling a given bandpass signal. The report was written in Italian and was known, at least, among the Italian community working on SODAR systems in which a few people and even students utilized my formulae in an unfair way because they did not mention the source. On 10 October and 7 December 1991, also to stop the above misuses, I sent two letters, containing my formulae for the undersampling, to EDN Signals & Noise Editor but I never received an answer. On 25 March 1994 I attended a Burr-Brown’s Applications Seminar in Rome, Italy, where I explained to the two relators my formulae. One of the relators, Mr. Jason Albanus, suggested to me to send my formulae to Mr. Jerry Horn at Burr-Brown Corp., Tucson, Arizona, for inclusion in future seminar books. I did this way but my letter was never acknowledged. Then on 11 July 1994, on Electronic Design, appeared an article by George Hill of Burr-Brown Corp., Tucson, Arizona, in which he exposed, at p.77, my formulae for undersampling, stating literally: ”After a recent applications seminar given by Burr-Brown in Rome, Italy, one of the attendees suggested an approach for easily calculating appropriate sampling rates for undersampling any specified range of input frequencies. He offered his ideas for inclusion in future seminars, but didn’t authorize us to use his name. Here is his approach…”. Of course I was that attendee and for me was clear that Mr. George Hill and everyone else should have used my name in connection with my formulae! For that on 13 September 1994 I wrote to Mr. George Hill inviting him to do so, but again there was no answer. Anyway, the formulae I proposed are the straightforward mathematical translation of the “accordion-pleated” (Ref.2) paper model, which is a direct consequence of Shannon and Nyquist theorems: it seems that the sampling theorem was formulated by Nyquist in 1928 and formally proven by Shannon in 1949. My interest on signal processing started in the mid of 1975 when I began doing my Physics thesis (Ref.5) which consisted in the design and in the realization of a SODAR system for use in atmospheric boundary layer studies. For the hardware I basically followed the work done by E.J.Owens (Ref.6), adding a few original solutions. During the 1976, and for many years after, this first version of SODAR and its upgrades were extensively used in measurement campaigns and at this point emerged the need of an efficient sampling and processing of the data, also because we had old computers with slow A/D and poor storage units! My first approach was hardware and I realized an audio heterodyne to translate down the spectrum of the signal. I was the first in Italy to build a SODAR system that worked well and even today many people use my scientific ideas and technical solutions even if not all of them recognize it. Of course the solution of the sampling problem was reached by successive approximations, and the final steps were taken between 1980 and 1981 when I ran into Ref.2, p.230, and imagined that the “accordion-pleated” paper model, that I named “soffietto” in Italian (Ref.4), had a useful mathematical formulation from which I deduced the formulae for undersampling. Only much more later I read Ref.1 and Ref.3 and realized that, at least the fundamental formula was already known, even if the topic was understated and treated differently and partially and without proof in the quoted references, instead I think that my proof is simple and smart. The Ref.1 stated the fundamental formula in a different form and in the time domain instead of the frequency domain, as I did. Furthermore no formula for is given. In the Ref.3 the undersampling (actually named “bandpass sampling theorem”) is listed among the problems left to the reader and the formula shown refers only to the lowest bound of the sampling frequency, but one of the terms may suggest, to an attentive reader, the way to compute . Then I think of my small contribution to the undersampling as simplifying and clarifying the topic for the practical use, but it should not be underevaluated or ignored or, worse, usurped.

Let be the lowest and the highest frequency of a band-pass signal to be sampled.

Based on the “accordion-pleated” paper model we should have and , with integer, to avoid the folding of the spectrum on itself. Simple manipulations give in which . For example, put , . Applying the second of the above formulae we obtain , i.e. , and then from the first we have all the allowable sampling frequencies: : , : and, of course, : . Based on the “accordion-pleated” paper model the order of the harmonics of the aliased spectrum of the bandpass signal could be reversed or not depending on the position of the original signal to respect to the chosen : if the corresponding is odd the order is preserved, if it is even the order is reversed. These calculations permit the adjustement of the sampling frequency depending on the specific application. If the data at our disposal are the bandwidth , and the carrier of the signal, we may put and , so that and and we can carry on the computation as above. Instead, the formulae reported in the cited article give the single value , being and . The formulae and can be easily deduced from . By definition therefore is always satisfied: note that you cannot use every for undersampling because you have to satisfy the other constraint. To deduce , assume , the arithmetic mean of the two bounds of the fundamental formula.

It is 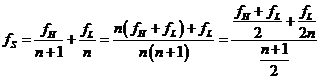. Putting and substituting we obtain 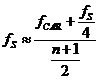. The substitution produces an lower than the arithmetic mean assumed before. It is and then with . A more direct way to obtain is to notice that with this particular sampling frequency the aliases of the spectrum of the signal are centred on the pages and its multiples (Fig.3, p.5, Ref.4).

It has to be from which .

REFERENCES

1. “Reference Data For Radio Engineers, Fifth Edition”, Howard W. Sams & Co., Inc., ITT, 1970, (p.21-14).

2. Julius S. Bendat, Allan G. Piersol, “Random Data: Analysis and Measurement Procedures”, Wiley-Interscience, 1971, (p.230).

3. E. Oran Brigham, “The Fast Fourier Transform”, Prentice-Hall, Inc., 1974, (p.87).

4. Angelo Ricotta, “Some remarks on the sampling and processing of SODAR data”, Technical Report, IFA-CNR, July 1983, (pp. 4-7, in Italian)

5. Angelo Ricotta, “Development of an acoustic radar and applications to the planetary boundary layer dynamics studies”, Physics Thesis, University of Rome, Italy, 1976 (in Italian).

6. E. J. Owens, NOAA MARK VII Acoustic Echo Sounder, NOAA Tech. Mem., Boulder, Colo., 1975.